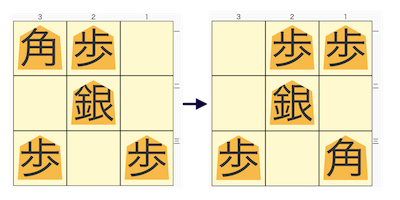
将棋パズルとは
数年前にTwitterで女流棋士の中倉彰子さんの呟きを見てその存在を知りました、最近書籍を出されたようです。子供の頃4×4の16マスのケースに1〜15までの数字が書かれたバラバラのピースを数字の順に並べ直すというパズルをやったことがありますが、それの将棋版と思えばいいと思います。但し盤面は3×3で先手番の駒だけを自由に配置し、スタートの局面から将棋の駒を動かしてゴールの局面に変化させるというもので、まず将棋の駒の動きを覚えないと出来ません。パズルの存在を知った時は解答を得るためのプログラムを作ろうなんて思いませんでしたが、3三将棋アプリを作った直後なので、プログラムに必要な部品が全て揃っているので作ってみました。
必要な作業
- 駒の動きを定義したPieceクラス(作成済み)
- 駒の制御を行うBoardクラス(作成済み)
- 盤面を多分木データとして格納するNodeクラス(今回作成)
- BFS(幅優先探索)で存在し得る全ての盤面を生成してNodeオブジェクトに追加
15ピースパズルや迷路を解く時なんかは1、2は不要なので簡単ですが、将棋パズル解答プログラムを一から作るとなると結構大変です。でも今回は前回の記事で使用したソースを若干修正してそのまま利用出来ます。
Nodeクラス
class Node
_counter = 0
_duplication = []
# 同じ駒が複数使用されていることもあるので座標も含めてソート
_sortCoordinate = (a, b) ->
kinds = ["Ou", "Hi", "Ka", "Ki", "Gi", "Ke", "Ky", "Fu"]
return kinds.indexOf(a["kind"]) - kinds.indexOf(b["kind"]) || a["posi0"] - b["posi0"] || a["posi1"] - b["posi1"]
# 局面を比較するためHashを生成
@make_hash = (board) ->
rec = []
for koma in board.pieces
buf = {}
buf["kind"] = koma.kind()
buf["turn"] = koma.turn
buf["status"] = koma.status
buf["posi0"] = koma.posi[0]
buf["posi1"] = koma.posi[1]
rec.push(buf)
rec.sort _sortCoordinate
return crypto.createHash('md5').update(JSON.stringify(rec)).digest("hex")
# 重複局面をチェックするために局面のHash値を追加
@set_dup = (hash) ->
_duplication.push(hash)
# 出現済みの局面ならtrue、新規局面ならfalseを返す
@check_dup = (hash) ->
check = (v for v in _duplication when v == hash)
if check.length > 0
return true
else
return false
# Boardオブジェクトとその子局面を格納するための配列を用意
constructor: (v) ->
@value = v
@child = []
# 答えの局面を探して見つけたら手数と局面を表示
search: (target) ->
return null unless target?
return @ if Node.make_hash(@value) == Node.make_hash(target)
ret = false
for v in @child
# 答えの局面を見つけた
if Node.make_hash(v.value) == Node.make_hash(target)
ret = true
_counter += 1
console.log("#{_counter}:")
v.value.display()
else
ret = v.search(target)
# 答えを見つけた後は、その過程の局面と手数を遡って表示
if ret
_counter += 1
console.log("#{_counter}:")
v.value.display()
break if ret
return ret
# 子局面を辿りながら多分木データを追加していく
add: (target, obj) ->
ret = null
for v, i in @child
# 親となる局面を見つけたらその子局面としてNodeオブジェクトを追加
if Node.make_hash(v.value) == Node.make_hash(target)
ret = v.child.push(obj)
# 見つからなければさらに子局面を辿る
else
ret = v.add(target, obj)
break if ret?
return ret
実行ファイル
# game.coffee
startTime = new Date().getTime()
bfs = (board) ->
queue = []
queue.push(board)
seq = 0
layer = 0
while queue.length > 0
bd = queue.shift()
layer += 1
for koma in bd.pieces
for v in eval("Piece." + koma.kind()).getD(koma.turn, koma.status)
buf = [].concat(koma.posi)
loop
break unless ((buf[0] + v.xd in [1..bd.cols]) && (buf[1] + v.yd in [1..bd.rows]))
buf[0] += v.xd; buf[1] += v.yd
dest = (o for o in bd.pieces when o.posi? && o.posi[0] == buf[0] && o.posi[1] == buf[1])
break if dest.length != 0 && dest[0].turn == koma.turn
if bd.check_move(koma, buf)
# 着手可能な手ならBoardオブジェクトをディープコピー(新たな局面を生成)
temp = bd.clone()
move_piece = (o for o in temp.pieces when o.posi? && o.posi[0] == koma.posi[0] && o.posi[1] == koma.posi[1])
temp.move_capture(move_piece[0], buf)
md5hash = Node.make_hash(temp)
# temp.display()
# 重複局面は多分木データに追加しない
if Node.check_dup(md5hash)
continue
else
Node.set_dup(md5hash)
seq += 1
if layer == 1
node.child.push(new Node(temp))
else
node.add(bd, new Node(temp))
queue.push(temp)
# console.log("seq = #{seq}")
break unless (dest.length == 0 && v.series)
# スタート局面
b = new Board()
b.pieces = []
b.pieces.push(new Piece.Ka(Const.FIRST, Const.Status.OMOTE, [3,1]))
b.pieces.push(new Piece.Gi(Const.FIRST, Const.Status.OMOTE, [2,2]))
b.pieces.push(new Piece.Fu(Const.FIRST, Const.Status.OMOTE, [3,3]))
b.pieces.push(new Piece.Fu(Const.FIRST, Const.Status.OMOTE, [2,1]))
b.pieces.push(new Piece.Fu(Const.FIRST, Const.Status.OMOTE, [1,3]))
# ゴール(答え)の局面
answer = new Board()
answer.pieces.push(new Piece.Ka(Const.FIRST, Const.Status.OMOTE, [1,3]))
answer.pieces.push(new Piece.Gi(Const.FIRST, Const.Status.OMOTE, [2,2]))
answer.pieces.push(new Piece.Fu(Const.FIRST, Const.Status.OMOTE, [3,3]))
answer.pieces.push(new Piece.Fu(Const.FIRST, Const.Status.OMOTE, [2,1]))
answer.pieces.push(new Piece.Fu(Const.FIRST, Const.Status.OMOTE, [1,1]))
node = new Node(b)
bfs(b)
node.search(answer)
# 一応最後にスタート時の画面も表示
b.display()
elapsed = new Date().getTime() - startTime
console.log "経過時間: #{elapsed}ミリ秒"
重複局面を除くことで答えの局面を探し出す際に最短手順であることが保証されます。
例題
実行結果
coffee game.coffee
1:
3 2 1
| |F|F|1
| |G| |2
|F| |M|3
2:
3 2 1
| |F| |1
| |G|F|2
|F| |M|3
3:
3 2 1
| |F|G|1
| | |F|2
|F| |M|3
4:
3 2 1
|M|F|G|1
| | |F|2
|F| | |3
5:
3 2 1
|M|F|G|1
| | | |2
|F| |F|3
3 2 1
|M|F| |1
| |G| |2
|F| |F|3
経過時間: 223ミリ秒
ゴールの局面からスタートの局面まで遡って表示されます。
最短手数になる原理
以前の記事にも書きましたが、BFS(幅優先探索)では局面を辿る順番が、一手目で現れ得る局面を全て辿った後に二手目の局面、二手目で現れ得る全ての局面を辿った後に三手目の局面と進んでいきますので、たとえ答えの局面に辿り着く経路が複数あったとしても答えに辿り着いた手順が最短経路であることが保証されます。答えに辿り着く手順が10手で完成する手順と15手で完成する手順があったとしても、BFSを使っている限り最短手数のものから見つかるからです。答えが見つかった時点で探索をやめればわざわざ多分木データを生成しなくてもいいのですが、せっかく全局面を探索してくれるので、このプログラムでは一旦全局面を保存してます。今回のNodeオブジェクトのような二つのメンバー変数を持つオブジェクトに全データを格納しておけば、いろいろな条件に当てはまる局面を探し出すのに便利で、最長手数を求めたりその手数で実現出来る局面を全てリストアップしたり出来ますので問題を作る時も便利です。
問題を作る
例えば以下のようなメソッドを追加してnode.recurCount(0)と呼び出せば、スタート局面から最短手順を選択した上で手数が最も長くなるのは何手かを求めることが出来ます。
recurCount: (cnt) ->
if _counter < cnt
_counter = cnt
cnt += 1
for v, i in @child
v.recurCount(cnt)
return _counter
先の例題のスタート局面から最も長い手数が必要となる局面は以下の局面で、必要な手数は9手です。
スタート局面から無駄に手数を伸ばすことなく最も手数がかかる局面をゴール局面とすれば難問が完成します。
もっと難問を作れるか
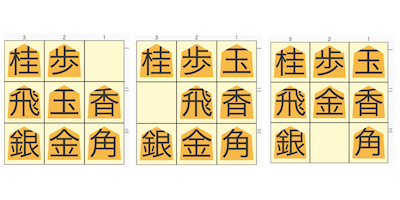
Twitterでゴール局面まで60手掛かるという難問を見かけたので、問題を作る側の立場で考えてみました。
まず全ての駒を適当に配置した問題を作って調べてみました。下の3パターンが上図をスタート局面とした場合の最長手数となる解答です。
手順は省略しますが上の局面から下の3つの局面に駒を移動させるには最短手数でも25手必要で、上のスタート局面から出現し得る全ての局面のうち25手かかるのは下の局面3つだけのようです。もちろん無理やり手数を伸ばして実現することは可能ですが、最短手順を選んでも25手かかってしまうというところがミソです。
ちなみにスタート画面の「歩」を「と金」に変えると最長手順は31手に伸びるようですが、長手順の難問を作るには適当に駒を配置するだけではダメなのかも知れません。3三将棋アプリを作った時に感じたのですが、「3三将棋(=9マス将棋)」だと適当に駒を配置するだけだと一目で正解が分かるような簡単な配置になってしまうことも多くて、熱戦が期待出来るような初期配置パターンを探すのに苦労しました。「将棋パズル」の場合も正解手順を見つけることより、長手順になる問題を見つける方が、問題を解くより難しいのかもしれません。最近はソフトで詰将棋を解くのは当たり前になってしまって、芸術的な詰将棋をソフトで作る研究が行われていると聞いたことがありますが、その状況と似ていますね1![]()
余談
自分のブログは「BFS DFS 違い」とか「BFS 用途」とかの検索ワードで来訪される人が偶にいるのですが、対戦ゲームに使用するとすればBFS(幅優先探索)の使い途は定跡データや学習データの格納・検索、DFS(深さ優先探索)の使い途は局面の先読み(MIN-MAX法を使った有利不利判定)ってことになるんじゃないでしょうか。進化する三目並べでも学習データの保存・検索にBFSを使用しています。
githubにソース公開(2021−07−15)
既に公開している3三将棋のソースを使えば記事で紹介しているプログラムを試せるのですが、若干の修正が必要になるので、githubに将棋パズル専用のリポジトリを作って纏めて公開しました。git cloneすればすぐにプログラムを試すことが出来ます。記事で触れている60手の長手数問題もコメント化して載せています。
結将棋アプリの全国ランキング問題を解かせてみたところ全問正解しました(ランキング1位を取れました)のでバグは今のところ無いと思います。結将棋アプリの全国ランキング問題(正解手順はすべて40手以下)を解かせてみて分かったのですが、問題を解くのに必要な時間が60手の長手数問題よりかなり長くなるものがあります。正解を得たところで終了せずに全局面を読んでいる所為もありますが、BFSでは読む深さよりも読む幅の多い問題ほど解くのに時間が掛かるということでしょう。