Project: GitHub
幅優先探索のメリット
アルゴリズムに関する本なんかを読んでいると、オセロゲーム、三目並べ、将棋などのいわゆる二人零和有限確定完全情報ゲームのソフトを作る時によく使用される「深さ優先探索(Depth First Search, DFS)」アルゴリズムとの対比で、「幅優先探索(Breadth First Search, BFS)」というアルゴリズムが紹介されていることが多いですが、かなり昔に読んだ本の中で強い対戦型ソフトを作るために幅優先探索(BFS)を使うと以下のようなメリットがあると書いてあった記憶があります。
- 思考時間に制限があるような場合は、深さ優先探索(DFS)だと偏った候補手しか読めないので時間に追われて悪手を選ぶことがあるが、幅優先探索(BFS)を使えばいつ読みを中断されてもそれなりに有効な一手を選ぶことが出来る。
- 序盤はBFSを使って広く浅く読み、終盤はDFSを使ってゲームの終局(詰み)まで読み切るように作れば強いソフトが作れる
なるほどそういうものかと納得し、今までずっと気にはなっていながらも、試してみる機会がありませんでした。また、自分が見てきた限りでは、書籍で紹介されているオセロや将棋のソフトでは、深さ優先探索(DFS)を紹介しているものばかり(いきなりαβ法とNEGMAX法を用いた最適解を紹介しているものがほとんど)で幅優先探索(BFS)を紹介しているものは見かけなかったので、今回自分で試してみることにしました。オセロや将棋ではなく例によって以前作った三目並べプログラムを題材にして試してみます。
対戦型ソフトと迷路は違う?
よく「最短経路の発見」、「迷路の解法」などを題材にしてBFSを使った解法とDFSを使った解法2つを比較しながら紹介している本を見かけるので、まずは現在DFSを使って動作している三目並べプログラムをBFSに置き換えただけのものを作ることにしました。一般にDFSとBFSの違いはデータ構造の違い(スタックを使うかキューを使うか)だけだと言われています。再帰関数を使って次々と局面をスタック(stack)に積み上げて先読みしていた部分を、同一局面を間引きながらキュー(queue)に追加&取得を繰り返すように変更することで実現できると巷の本には書いてあります。そして以下のような感じで、幅優先探索を使って全局面を辿っていく手順は実現出来た(実際に動作確認したい人はgithubからソースコードを取得してください)のですが、局面を評価して手を選ぶ処理を書こうと思った時にちょっとおかしいと気がつきました。
def bfs(board, turn)
init_dup
queue = Array.new
board.teban = turn
set_dup(board); queue.push(board)
locate = nil
while queue != [] do
buf = queue.shift
#キューから一局面を取り出して一手ずつ打つ
buf.each_with_index {|b, i|
#既に駒があれば次の場所へ
next if b
temp = buf.clone
temp[i] = buf.teban
#同一局面があれば次の局面へ
next if check_dup(temp)
temp.teban = (buf.teban == CROSS) ? NOUGHT : CROSS
#DFSならここで評価関数を呼んで手を選択する
??????
set_dup(temp); queue.push(temp)
}
end
DFSの場合なら、勝ちか負けか引分けかの3値のうちどれかを返す読み切り用の評価関数を呼び出して、先手なら評価値が大きい方後手なら小さい方を選ぶという処理を書くだけで、先手番の局面・後手番の局面と実際に人間がゲームを進める時のように交互に局面を評価しながら辿っていくのに対して、BFSで同じようにコードを書くと、一手目に現われ得る全局面を評価&比較し、それが終わったら二手目の全局面を評価&比較するという順序で局面を辿っていくため、お互いに最善手を打つというMIN-MAX法のロジックが働いていません。とりあえずBFSで書き換えたものを実際に動かしてみても非常に弱いプログラムになります。
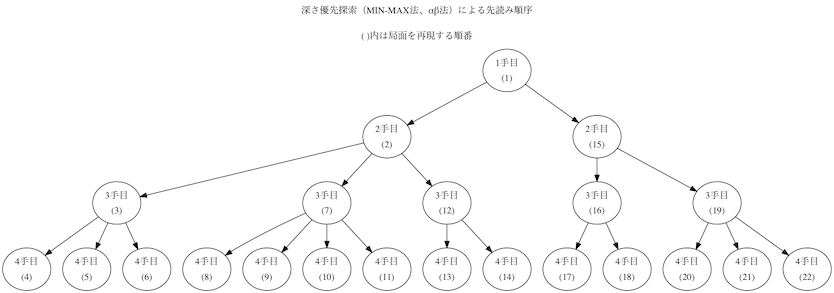
- DFSの先読み順序
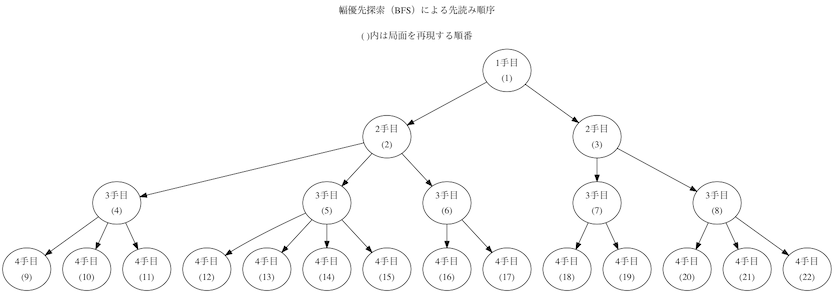
- BFSの先読み順序
なぜBFSだと弱いのか考えてみると、まず一手目、二手目という勝負がつかないところの評価はDFSもBFSも同じですが、勝負がついた時の評価がDFSだと局面を評価した後に一手前に戻った時(スタックからpopupした時)に評価値を比較して相手に有利だった場合にその手を避けることが出来るのに対して、BFSだと勝ちなら勝ち、負けなら負けの評価のまま上書き(比較する時に等号があれば上書き、無ければ無視)し続けることになります。それに一手前に戻って選択した手を変えることがないということは、BFSで勝ちの評価を得た局面に至ったとしても、それは相手が自分にとって有利な手を打ってくれたからこそその局面になった可能性が高いわけです。この点が迷路を解くのと違うところだと思いますが、迷路の場合は普通は正解が一つでその正解手順を発見した時点で先読みを打ち切ればいいわけですが、三目並べ等の対戦ゲームの場合は勝ち局面に至る手順が一通りではなくかなりの数になリ、勝ち局面に至ったといっても相手がお手伝いしてくれている場合が多いのです。将棋で「二人掛かりで玉を詰める」などとヘボ将棋を揶揄することがありますが、まさにそういう状態で勝ち局面を発見して「自分の勝ちだ」と評価して手を選んでいる状態がBFSの手順になります。
また、上の図の先読み順序の違いを見れば、時間制限があるような時にBFSだと確かに思考をいきなり中断された時に安定した評価を得られそうですが、その評価が独りよがりの評価になっているのでは意味がありません。仕方がないので、使用する評価関数を勝ち、負け、引分けの3値を返すものから、重み(真ん中が2点、角が1点、辺が0点)による評価関数に変えて序盤(3手目まで)をBFSで読み、3手目以降はDFSで読んで手を決定するようにしました。でもこれは重みによる評価関数を使用すればBFSによる先読みが有効に働くというわけではなく、BFSを使用している限り独りよがりの読みになっている点は同じなのですが、以前記事に書いたように初手からDFSで読み切ると勝つことを諦めてしまって、勝つ可能性が高くなるにもかかわらず初手に真ん中を選んでくれないので、重みによる評価関数を使って初手に真ん中を選ぶようにしているだけです。でも初手に真ん中を選ぶようにするだけなら評価関数だけを変えればいいことで、先読みアルゴリズムをDFSからBFSに変更する必要はありません。つまり今githubにアップされているソースはせっかく作ったからBFSのロジックを組み込んでいるだけと言えます1。
まとめ
結局、冒頭に書いた幅優先探索のメリット1も2も一見正しいように思えるけど、BFSだけでこのメリットを実現することは無理そうです。もう昔のことでこのメリットについてどこで読んだのかも覚えていないのですが、まずBFSで局面を絞った後で、その絞った局面からMIN-MAX法を使って先読みを続けて手を決めるというような趣旨だったかもしれません。でもまぁ今回実際にプログラムを書くことによって、迷路を解くのとは違う問題があることを知ることが出来ました。
ネットで検索してみると幅優先探索を使用していて尚且つ強い(であろう)オセロプログラムについての記述を見つけることができました2が、どのように強くしているか詳細はわかりません。でも「定石」と「学習」という単語が出てきているのでBFSで形成したツリー構造に定跡データを格納して利用するということかもしれません。単に定跡データを格納しておくだけなら起動時にデータとして読み込めばよく動的にツリー構造を辿る必要はないので、学習しながら保存するということなのでしょう。確かにそういう使い方なら納得できます。
もう一つのまとめ
アルゴリズムに関する本には「DFSとBFSは使用するデータ構造が違うだけ」なんて書いてあるからDFSで出来ることは当然BFSでも同様に出来るはずだと私が思い込んでいたせいもありますが、そもそもBFSは探索アルゴリズムなので勝ち局面に至る最短の手順を探索出来ていると考えるべきかもしれないと、ここまで書いてから思い始めました。BFSだと独りよがりの評価しか出来ないなんて言われる筋合いのものではなく、双方が協力した場合の最短の経路(勝ち手順)を探すことが出来ていると考えるべきなのでしょう。確かにBFSだけで対戦ゲームプログラムを強くするのは難しそうですが、逆にDFSアルゴリズムを使ってBFS同様の独りよがりの評価をする弱い状態(「二人掛かりで玉を詰める」状態)に変更するのは簡単です。
そう考えると、DFSという単なる探索アルゴリズムを使って人間が考えるような「相手が有利になる手を避ける」、「双方が最善手を打つ」というロジックを簡単に実現出来ることの方が例外的なことなのかもしれません。単なる探索アルゴリズムでしかないはずなのにあたかも人間が思考しているようなプログラムの振る舞いを実現できるからこそ、DFSを使ったプログラムがAI(人工知能)と称される3のかもしれません。
私は学者じゃないので詳しくはわかりませんが、ちょっと穿った見方をすれば、人工知能という単語を使った方が予算が獲得し易いとか本を売り易いとかいう事情があって、少々大げさなのは承知の上で積極的に「人工知能」という単語が使われてきたのかもしれません。