MIN-MAX法とαβ法

MIN-MAX法

　MIN-MAX法とは、オセロゲームなどのある局面で先手、後手、どちらが有利か判断する評価関数を用意し、先手、後手が互いに最善手を打つと仮定して先読みを行うアルゴリズムです。先手をプラス方向の値（MAX値）後手をマイナス方向の値（MIN値）で評価することが多いようです。
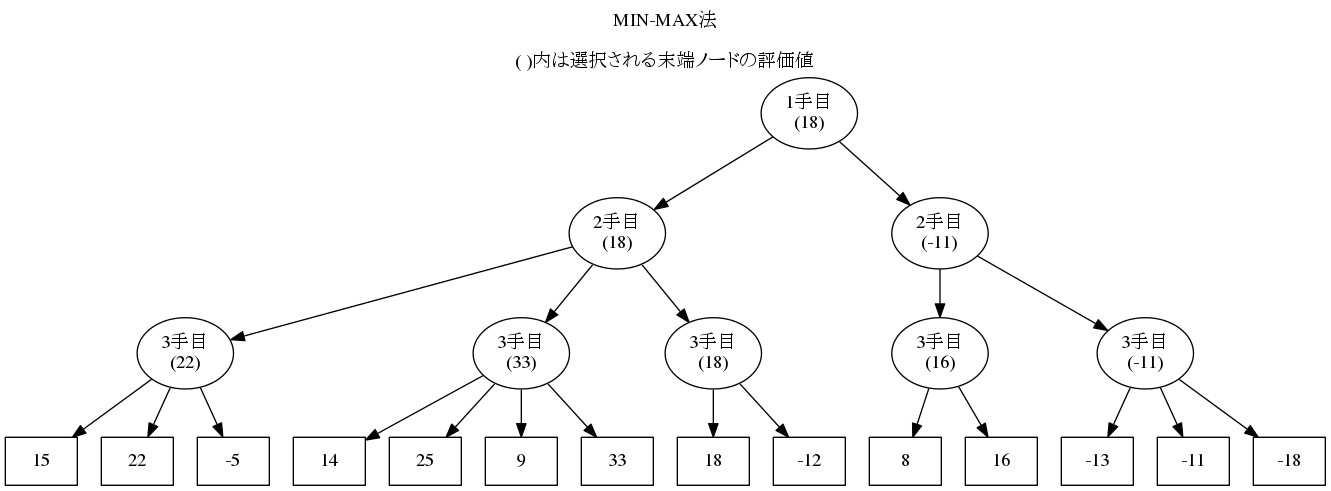
　上の図はオセロゲームで3手読みをする場合の例ですが、◯図形はオセロの一局面（ノード）で□内の数字が3手目を打ったときの評価値になります。3手目と書いてあるノードは先手が打つことが出来るすべての手を順番に評価していくためのループで、2手目となっているノードが後手が打つことが出来るすべての手を順番に評価していくためのループです。実際のプログラムではこのツリー構造を左から右の順に局面を評価していくことになります。
　全体図は1手目を先手が打った場合に後手が2手目を打つことが可能な手が2通りあり、その後先手が打てる手がそれぞれ3通り、2通りあることを表しています。まず左側のtreeを見ていくと、3手目に先手が打った局面で評価関数を呼ぶと15、22、-5という3つの評価値が得られたということです。で、先手は自分にとって最善手である一番評価値が高い22の局面を選び、取りあえずその評価値と指し手を記憶しておきます。次のノードで同様に3手目まで手を進めて14、25、9、33という4つの評価値を得て先手が選んだ最大値33と先ほどの評価値22を比較して、後手は自分に取って最善手である小さい方の22を選ぶという具合です。先手（3手目）では最大値、後手（2手目）では最小値を選択するというやり方で進めて、評価値が18という左側のtreeの2手目の評価が完了します。次に、右側のtreeでも先手（3手目）は最大値、後手（2手目）は最小値を選び-11という評価値が残ります。最終的には18と-11を比較して先手は大きい方の18を選び、1手目の先手の評価が完了します。
　最終的に指し手を決めるまでに、3手目の局面の数の分だけ評価関数を呼び出したことになるので、1手目の評価が完了するまでに14局面評価したことになります。

αβ法

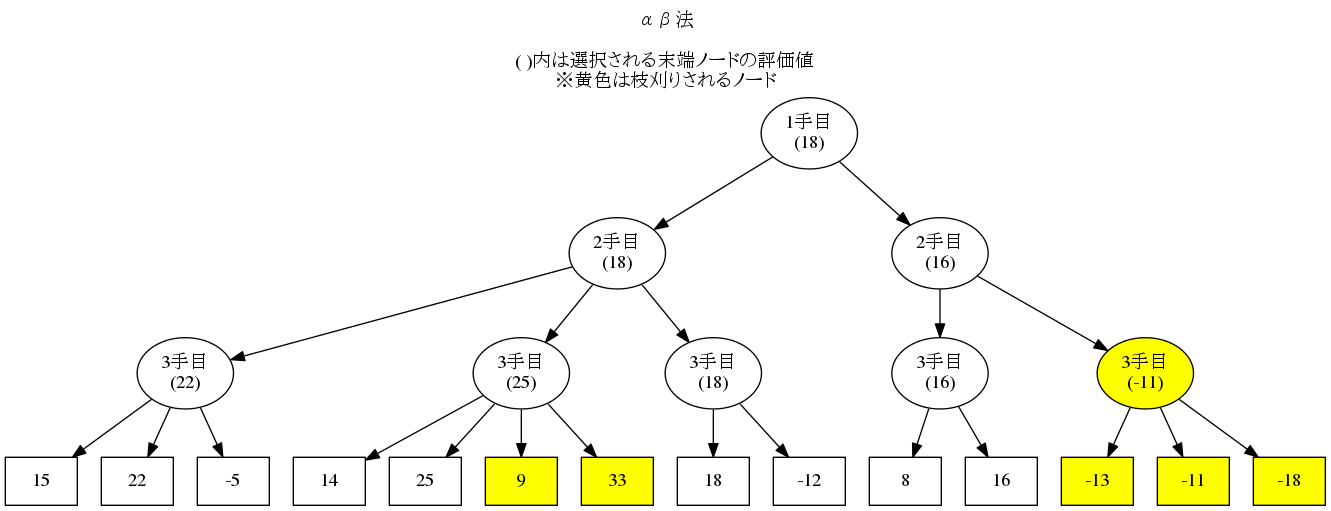
　αβ法はMIN-MAX法と同じ結果を得られるにもかかわらず、局面を枝刈りすることで時間短縮が出来るというすばらしいアルゴリズムです。なぜ局面の枝刈り（評価の回数を減らす）をしながら同じ結果が得られるのか見ていきましょう。
　まずMIN-MAX法と同様に左の3つの評価値から22という評価値が得られます。この22を基準値として読み進めると14、25という評価値を得ますがこの25という評価値を得た時点で、このノードは選ばれないことがわかります。なぜなら一つ上の後手のノードでは常に最小値を選ぶからです。この先読み進めて25より大きい評価値を得られたとしても一つ上の後手のノードで、22より大きな値が選ばれることはないので、ここで読みを打ち切っても問題ない（MIN-MAX法と同様の結果が得られる）わけです。これをβカットと言うそうです。その後同じく22を基準値として、次のノードに移り18という評価値を得ますが、18は22より小さいのでそのまま読み進みます。そして18と-12の大きい方である18が選ばれ、後手のノードで18と基準値の22を比較し小さい方の18が選ばれます。これで2手目の候補手が一つ決まりました。
　次に右サイドのtreeに移りますが、1手目の候補手から読み直すので、基準値は無く新たに末端ノードの3手目を順に評価することになります。得られた8と16を比較して先手（3手目）では最大値である16が選ばれます。16という後手の候補手が一つ得られたわけですが、後手の候補手はより小さい評価値が選ばれるわけですから、今のノードから分岐する3手目をいくら読み進んでいっても16以上になることはないということがわかります。そして一つ上の1手目の先手のノードでは先程の評価値18と比較して大きな方が選ばれることが分かっているわけです。つまり18より小さい評価値が後手（2手目）の候補手に一つでも現れた時点で、この後手のノードから分岐する先の手は読む必要がないことがわかります。これをαカットと言うそうです。ということで先程の18と今読みを打ち切った16を比較して、MIN-MAX法と同じ18が選ばれます。
　この例ではMIN-MAX法と比較して評価関数を呼び出す回数を5回減らすことが出来ただけで、それほど有り難みが伝わらないかもしれませんが、例えば一局面で選択できる手が3手だったとして3手先まで読むとMIN-MAX法だと\(3^3\)回（27回）評価関数を呼ぶことになりますが、評価する局面の順番が理想的な場合αβ法だと\(3^\frac{3}{2}\)回（約6回）で済むそうです。前回記事で紹介した三目並べのプログラムの例の場合、まさにこれぐらいの高い効果が得られたと思います。

「HTML5+CoffeeScriptで作る最強の三目並べプログラム」

オセロと将棋の違い

　今までにいろんなプログラミング言語でオセロを作った経験があるのですが、オセロを作った同じやり方で三目並べを作るとうまく出来ませんでした。三目並べを作った顛末はここに書いていますが、どのような問題があったかというと、オセロの局面の評価は末端ノード（葉）で行うため、三目並べで同様の作り方をすると途中でラインが揃って勝負がついているにも関わらず先読みを続けてしまうという不都合が起こり、間違った結果が返ってきます。各ノードで局面の評価を先にしてから先読みを続けるかどうか判断するという作り方にしなければなりません。その違いに気づくまで私は結構悩みました。
　将棋も三目並べと同じでゲームがいきなり終了する（詰み）ことがあるので、有限手数先を読みそこで評価する作り方をしているとあり得ない局面を読んでいて間違った評価をすることになります。では、オセロはゲームがいきなり終了することは無いのかというとそうでもなく、頻度は低いと思いますがオセロにもパーフェクトで勝負がつくケースというのがあるので、その対策は必要です。でも自分がオセロプログラムを作った経験から言うと、特にパーフェクト負けへの対応をしていなくても自然と回避されるケースが多いと思います。巷に出回っているオセロのソフトも偶々うまくいっているというケースが多いのではないでしょうか。
　もう20年以上前のことですが、自分が作ったオセロプログラムがどれほどの強さなのか他のプログラムと手動で対戦させていた頃、とても強くて自分が作ったソフトは歯が立たないフリーソフトがあったんですが、そのソフトに自分の作ったソフトが何度か序盤でパーフェクト勝ちをしたことを思い出しました。その強いオセロソフトはパーフェクト負けへの対応をしていなかったのでしょう。三目並べを作って見るまではオセロも三目並べも将棋も同じようなゲームだと思っていたのに、そんな違いがあることに今更ながら驚きました。