気になることがまだ残っている
前回の続きです。手数毎に報酬や罰の値を変更する方法をいろいろ試しましたが、大した成果が上がらなかったので、もとに戻して(全ての局面データに一律に報酬や罰を与える方法、前々回までの状態に戻して)他の切り口から気になっていたことを試してみたいと思います。
もしかしたら三目並べに最善の強化方法というものが既に確立されているのかもしれませんが、自分で試してみたいので続けます。
強い人ほど短手数で勝つはず?
以前から気になっていたのですが、完全読み切りプログラムでは、先手( X )の時に以下のような経過を辿って勝つ時があります。
初期盤面 1手目 2手目 3手目 4手目 5手目
|1|2|3| |1|2|3| |1|O|3| |X|O|3| |X|O|O| |X|O|O|
|4|5|6| -> |4|X|6| -> |4|X|6| -> |4|X|6| -> |4|X|6| -> |4|X|6|
|7|8|9| |7|8|9| |7|8|9| |7|8|9| |7|8|9| |X|8|9|
4手目で”9”の場所を選べば勝ちなのにそこを選ばずに”7”の場所を選んでダブルリーチをかける時があるのです。完全に読み切っているために”7”の場所も”9”の場所も同じ評価値(どちらを選んでも勝ちであることを読み切っている)なのでこういうことが起きるわけです。事前に勝ちがあるかどうかを判断して、勝ちがある時はその手を優先して選択するように変更するのは容易ですが、機械学習プログラムの場合は先読みするわけでは無いので、こういうケースに対処するために「なるべく短手数で勝負を終える方がいい」と学習させる必要があるのではないかと思ったわけです。機械学習プログラムの場合は先読み関数を使用せず、過去の経験から学習して手を選択するだけなので、勝負が長引けば間違える(悪い手を選択する)可能性も高くなります。短手数で決着したゲームの方が長手数の時より報酬を多めに与えるべきか、本当は手数と強さの相関関係を調べた方がいいのかもしれませんが、実際に試した方が早そうです。将棋などでも必ずしも強い人の総手数が短いとは言えないと思いますが、詰みがある時は逃さないという意味では「強い人は短手数で勝つ」ということが言えるような気もします。
ということで、いたずらに勝負を長引かせないために、なるべく短手数で勝った時の方が報酬を多く与えるように学習機能(「強化」の方法)を変更して効果を確認してみました。
#変更前
inc = (@sengo == CROSS) ? 3 : -1
↑こんな感じになっていたコードを以下のように変えただけです。
#変更後
base = SHORTEST / history.size
inc = (@sengo == CROSS) ? (3.0 * base) : (-1.0 * base)
SHORTEST定数は最短で勝負がついた場合の手数6(初期盤面を含む)です。総手数を分母にしているので、最短手数の6手で勝った時だけ報酬が+3されますが、手数が伸びるほどそれ未満の報酬しか受け取れなくなります。また、短手数で負けた時ほど罰が厳しくなります。最短手数で負けた場合は辿ったすべての局面データから、選択した場所の小石(score配列)が−1されていきますが、最長手数10手(初期盤面を含む)で負けた時は0.6 (\(-1\times\frac{6}{10}\) ) ずつしか引かれません1。
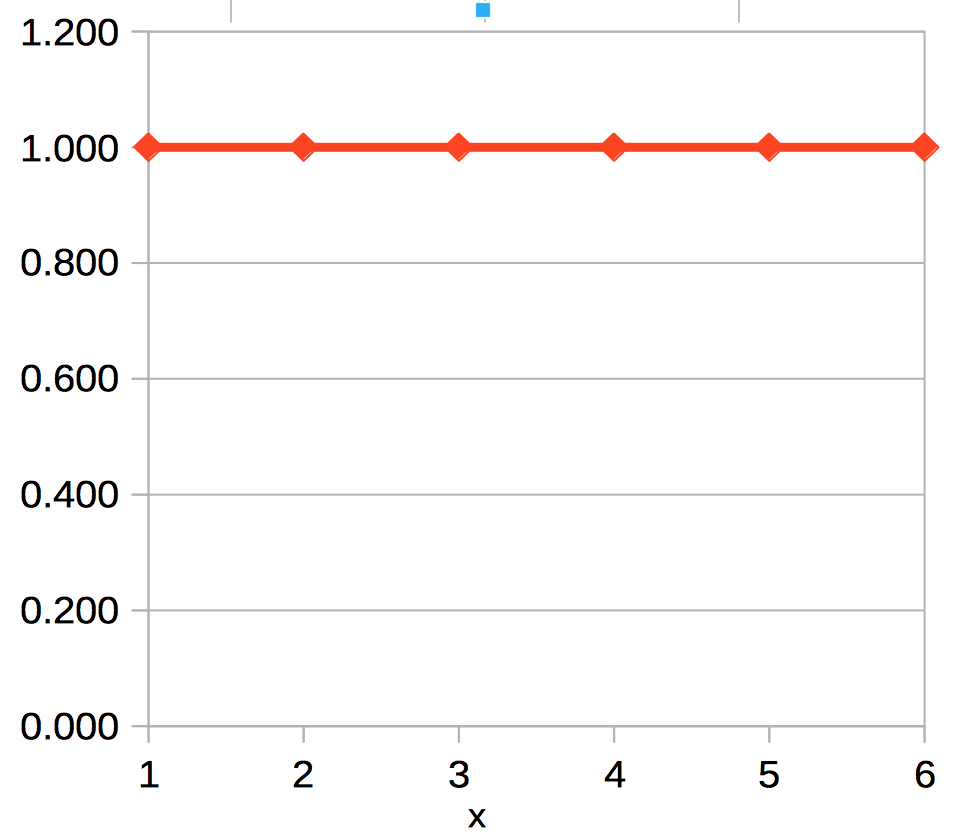
これは手数によって(何手目かによって)報酬や罰を変化させるわけではないので、前回の記事の方法と似ていますが違います。何手でゲームが終了したかによって y の値が変わる横一直線のグラフになり、前回同様6手で終了した場合を敢えてグラフ化すると、以下のようになります。
対戦結果は以下です。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 短手数の報酬を多くした強化学習 | 0勝8,807敗91,193分 | 64,978勝23,394敗11,628分 |
負け数が減って学習効果が上がったようですが、乱数プログラムとの対戦成績は若干勝率が悪くなっています。
終盤の一手の価値を上げる?
前回の記事で終盤の手ほど重要視して報酬や罰を増やす方法を試しましたが、今回は報酬や罰は変えずに終盤ほど小石(score配列)の総数を減らすという方法を試してみます。
「STATISTICS HACKS」には以下のように書かれています。
3目並べのケースでは、すぐに負けにつながるミスを効率的に処分し、罰するべきだ。ゲーム終盤の手で使うビーズの総量が少なければ、より短期間で学習されていくはずだ。
強化学習の際に初期盤面や一手目の局面は頻繁に現れますが、組み合わせの数が多い中盤・終盤の局面は出現頻度が低いのでなかなか学習が進まないので学習効果を上げるためにその局面に配置されている小石(score配列)の総数を少なくすればいいというわけです。
全局面の多分木データを生成する際(Player.bfsメソッド)に小石の初期値を何手目の局面かによって変えるようにしました。初期盤面は10個、1手目の局面は9個というように手数の深さによって減らしていきます。それと小石が不足した際に補充する時(Player.learningメソッド)も局面の深さによって補充する小石の数を初期化時と同様に変える(減らす)ようにしました。
#Player.bfs
#変更前
@trees.add(buf, Tree.new(temp, PEBBLES))
#変更後
@trees.add(buf, Tree.new(temp, PEBBLES - layer + 1))
#Player.learning
#変更前
while board
#石が0個になっていたら置ける箇所全てに追加
if buf.score[pre_index] <= 0
buf.score.map!{|v|
v += PEBBLES if v
}
}
#変更後
pebbles = history.size
while board
#石が0個になっていたら置ける箇所全てに追加
if buf.score[pre_index] <= 0
buf.score.map!{|v|
v += pebbles if v
}
}
報酬や罰に関しては、勝ちは+3、負けは−1、引き分けは+1という「従来の強化学習」と全く同じだということです。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 短手数の報酬を多くした強化学習 | 0勝8,807敗91,193分 | 64,978勝23,394敗11,628分 |
| 手数によって小石の数を減らした強化学習 | 0勝7,977敗92,023分 | 67,356勝21,444敗11,200分 |
前回の記事を含めて、今までで一番効果が出ました。どうやら報酬や罰の与え方を変えるより、小石の総数を減らすことの方が効果があるようです。
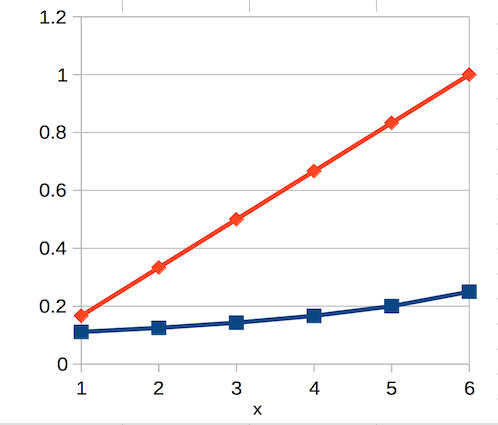
ところで「初期状態や補充分の小石の数を手数によって変化させて、報酬や罰は一定量にする」ことと「初期状態や補充分の小石の数は一定にして、報酬や罰を手数に応じて増減させる」のとどう違うのか、前回のようにグラフの傾きで考えてみると、総手数が6手(初期盤面含む)で終了した場合、小石の総数は初期盤面では9箇所×小石10個、1手目の局面では8箇所×小石9個、2手目の局面では7箇所×小石8個、となるので数の推移は以下の表の y′ のようになり
| x | y | y′ |
|---|---|---|
| 1 | 0.167(1/6) | 0.111(10/90) |
| 2 | 0.333(2/6) | 0.125(9/72) |
| 3 | 0.500(3/6) | 0.143(8/56) |
| 4 | 0.667(4/6) | 0.167(7/42) |
| 5 | 0.833(5/6) | 0.200(6/30) |
| 6 | 1.000(6/6) | 0.25(5/20) |
グラフにすれば以下のようななだらかな曲線になりますが、
これには途中の補充分が考慮されていないのであまり意味がありません。一応前回のように回帰方程式を使って対戦させてみましたが全然ダメでした。ゲームが終了する度に評価を実施(Player.learningメソッド)し報酬や罰を加算するわけですが、小石が補充される機会というのは毎回ではありません。でも、補充される度に今までより小石の総数が抑えられるのでかなり影響しているはずでが、計算がややこしそうだったので比較は諦めました。
とにかく、前回の記事からいろいろと報酬や罰の与え方(グラフの傾き)を弄っていましたが、大事なのはそんなことではなく、如何にして小石の総数を減らすかだということがわかったということです。
確認のため、終盤を重視したり短手数の時に報酬を増やしたり余計なことはせず「従来の強化方法」(手数に関係なく一律に全局面の小石の数を増減させる方法)で、小石の初期値と補充分の定数を10から1にだけ変更して試したところ、以下の表のように断トツで今までで一番良い結果が出ました。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 短手数の報酬を多くした強化学習 | 0勝8,807敗91,193分 | 64,978勝23,394敗11,628分 |
| 手数によって小石の数を減らした強化学習 | 0勝7,977敗92,023分 | 67,356勝21,444敗11,200分 |
| 小石の初期値と補充分を10から1に修正 | 0勝3,526敗96,474分 | 77,058勝12,829敗10,113分 |
勝ちは+3、負けは−1、引き分けは+1という報酬や罰の与え方(グラフの傾き)を変えることで学習効果に多少の改善があったとしても、そんなものは小石の総数を減らすことに比べたらわずかな効果しかないということでしょう。
今から思えば小石が不足した時に補充するやり方に修正した時点(前々回の記事)で、初期値を10から1にすればよかったです。
終盤の手ほど重要視する方法は効果がない?
小石の総数を減らすことが強化学習の効果を上げるのに有効なことはわかりましたが、前回の記事で試していた終盤の手ほど重要視する(終盤ほど報酬や罰を増やす)方法が否定されたわけではありません。それを確認するために、小石の初期値や補充分を10個から1個に修正した上で、尚且つ前回の方程式1(\(y = \frac{1}{総手数} x\))を適用して確認してみました。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 小石の初期値と補充分を10から1に修正 | 0勝3,526敗96,474分 | 77,058勝12,829敗10,113分 |
| 終盤の手ほど重要視(線形関数)Part 2 | 0勝2,068敗97,932分 | 80,512勝11,417敗8,071分 |
予想通り対最強プログラムでは負け数が減り、対乱数プログラムでも勝率が上がっていますので、全部は試しませんが前回の記事で使用した他の方程式を適用しても前回同様の傾向が出るのだと思います。
次に、今回の記事で最初に試した「短手数のゲームほど報酬や罰を増やす」方法も試してみました。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 小石の初期値と補充分を10から1に修正 | 0勝3,526敗96,474分 | 77,058勝12,829敗10,113分 |
| 終盤の手ほど重要視(線形関数)Part 2 | 0勝2,068敗97,932分 | 80,512勝11,417敗8,071分 |
| 短手数の報酬を多くした強化学習 Part 2 | 0勝2,433敗97,567分 | 78,953勝11,249敗9,798分 |
やはり、単に小石の総数を減らしただけより、対最強プログラムでは負け数が減り、対乱数プログラムでも勝率が上がっているので、効果が出ています。
小石を浮動小数点数で扱うように変更した甲斐がありました2。
人間並みに強くするにはどれぐらい学習が必要か?
「STATISTICS HACKS」の仕様に沿いながらこの三目並べ機械学習プログラムを初めて作った時点では、完全読み切りの最強プログラムとの対戦成績は8割の引き分け率でしたが、いろいろ弄って9割7分まで上げることが出来ました。三目並べを人間同士で対戦すればほぼ100%引き分けになると思いますが、うっかりミスもあるので、9割7分の引き分け率というのはほぼ人間並みになったと言えるのではないでしょうか?
でも、三目並べで10万回も対戦(学習)させてようやく9割7分になる3というのは、機械学習プログラムの出来としてどれほどのものなのかわかりません。学習効率を数値化して競う大会なんかがあっても面白いかなと思いました。ただ、麻雀ソフトなんかでもそうですが、三目並べだとズルをすれば簡単に強く出来るのでチェックが大変かもしれません。
結局、ソフトウェアとしての出来の良さを競うのであれば、将棋や囲碁のように完全読み切りが不可能なゲーム(ズルが出来ないゲーム)を題材にして、強さを競うという形が分かり易く現実的なのかもしれません。