闇雲ってこういうことかも
次に記事を書く時は別の話題にしようと思っていたのですが、三目並べの強化学習に関して試さずにはいられなかったので、闇雲と言われようが思いつくままにやってみたことを書いておきます。
以前、「STATISTICS HACKS」の中で序盤より終盤の手を重視する方法について記述されていることに触れました、そして今まで試した方法は報酬を与えるにしても罰するにしても選択した全ての局面で同じ値を加算したり減算したりしていましたが、今回は手数毎に違う値を加減算する方法を試してみました。
終盤の手ほど重要視すべき?Part 1
「STATISTICS HACKS」には以下のように書かれています。
動物が学習する手法をまねたい場合、ゲーム終盤近くの手が、ゲーム序盤よりも重大であるようなシステムに調整してもよい。これは行動が適切な時期に近いほど、その行動を強化する効果が最大になるという観察結果を反映することを意図したものだ。
現時点の機械学習プログラムは、勝負がついた時点で局面を初期盤面まで遡りながら局面に配置されている小石(score配列)の数を増減させて学習効果を反映させる仕様です。勝った場合は、一つ手前の局面の9個ある配列データ(score配列)の内、選択した手の場所の値を増やして(報酬を与えて)次からもその局面では再度その手を選ぶ確率を上げるようにするわけです。そしてその前の局面、その前の局面と遡りながら同じように数値を加減算していきます。でも、以前の記事にも書きましたが、辿った全ての局面のデータを一律に同じ数だけ増やして(あるいは減らして)いくというのは確かに少し疑問を感じます。例えば相手の石が揃うのを防がなかったような場合、その手は大悪手であるにも関わらず、序盤の一手と同様の罰しか受けないわけで、感覚的にはそれでいいの?って感じです。だから、ここに書かれているように、報酬も罰も終盤ほど大きな値になるように調整してみました。
まず、最終手が1になるように1を手数で割った値を係数にして、勝ちなら3負けなら−1を掛けた値を反映させるようにしてみました。x 手目の局面の報酬を決めるための係数を y で表します。
\(y = \frac{1}{総手数} x \hspace{3.5em}\tag{方程式 1}\)
最短手数6(初期盤面を含む)で勝負がついたとすると、最終手番の局面は x = 6 で y = 1 となり、勝った場合は\(y\times3=3\)、負けた場合は\(y\times-1=-1\)の値を各局面のデータ(score配列)に加算します。その一つ前の手番のデータはx = 4, y = \(\frac{4}{6}\)となり、勝ちなら\(y \times3=2\)、負けなら\(y \times -1=-0.6666\)が加算されます。
例えば10手(初期盤面を含む)で学習ソフトが勝ったとすると、最終盤面から初期盤面まで順番にソフトの手番の局面データに \(3, 2.4, 1.8, 1.2, 0.6\)の値が加算され、終盤の局面ほど大きな報酬が与えられるわけです。
総手数6手で終了した場合の係数(求める値 y は、あくまで3や−1に掛ける係数です)は以下の方程式で表され
| x | y |
|---|---|
| 1 | 0.167 |
| 2 | 0.333 |
| 3 | 0.500 |
| 4 | 0.667 |
| 5 | 0.833 |
| 6 | 1.000 |
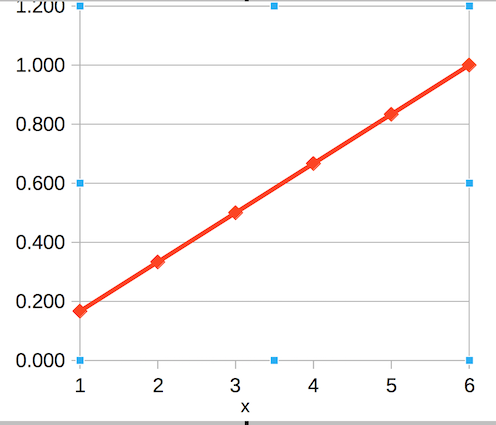
グラフにすると下のようになります。
この状態での対戦結果は以下のようになりました。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 終盤の手ほど重要視(線形関数) | 0勝8,334敗91,666分 | 61,383勝26,053敗12,564分 |
若干ですが最強プログラムとの対戦成績は向上したようですが、乱数プログラムとの対戦成績(=学習効果)は悪化しました。
終盤の手ほど重要視すべき?Part 2
10万回の対戦の途中経過を観察していないのではっきりとは言えませんが、終盤の手ほど重要視するようにはしてみたけど劇的に学習効果が上がるってわけでもなさそうです。でも、終盤を重要視すると言ってもPart 1 のように等間隔の増分でいいのでしょうか?1手目、2手目、3手目と等間隔で手の重要度が変化するとはとても思えません。相手のラインが揃うのを防がない手を選択して負けるケースなんかを考えると最終手は段違いに重要な気がします。
ということで、指数関数的に指し手の重要度が増すと仮定して方程式を改造しました。総手数6手(初期盤面を含む)でゲームが終了したとするとPart 1 の方程式の値は以下のように等間隔で推移( y の値)しますが、
| x | y (Part1) | y′ |
|---|---|---|
| 1 | 0.167 | 0.050 |
| 2 | 0.333 | 0.100 |
| 3 | 0.500 | 0.200 |
| 4 | 0.667 | 0.400 |
| 5 | 0.833 | 0.800 |
| 6 | 1.000 | 1.050 |
その横に y′ としてこんな感じになるんじゃないかという値を捏造して、その値をLibreOffice(Excelでも可)を使って回帰して得られた方程式が以下のものです1。
\(y = 0.029 \times 1.882^x \hspace{3.5em}\tag{方程式 2}\)
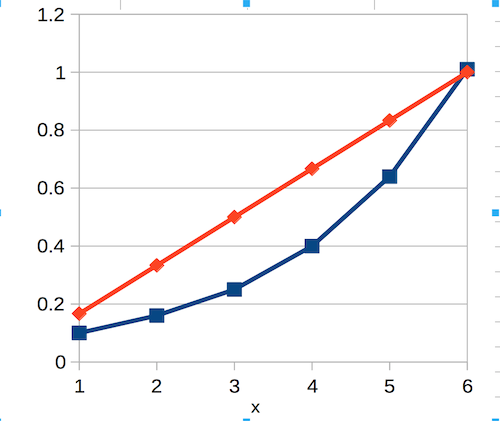
グラフは以下の青のラインです
対戦結果は以下です。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 終盤の手ほど重要視(線形関数) | 0勝8,334敗91,666分 | 61,383勝26,053敗12,564分 |
| 終盤の手ほど重要視(指数関数、小) | 0勝8,863敗91,137分 | 59,992勝25,810敗14,198分 |
報酬や罰が等間隔で配分される線形関数の時より、対最強プログラムも対乱数プログラムも勝率が落ちてしまいました。でも最強プログラムとの対戦成績に関しては「従来の強化学習」よりいい成績なので、この時点では一応効果はあると思っていました。
終盤の手ほど重要視すべき?Part 3
指数曲線にした方が勝率(というか引き分け率)が落ちてしまったのは回帰曲線が線形関数を下回っているのがよくないのかと思って、もう一度値を弄って重みを掛ける係数の値が線形関数の上にくるようにしてみました。
| x | y (Part1) | y′(Part2) | y′′ |
|---|---|---|---|
| 1 | 0.167 | 0.050 | 0.300 |
| 2 | 0.333 | 0.100 | 0.480 |
| 3 | 0.500 | 0.200 | 0.750 |
| 4 | 0.667 | 0.400 | 1.200 |
| 5 | 0.833 | 0.800 | 1.920 |
| 6 | 1.000 | 1.050 | 3.030 |
\(y = 0.188 \times 1.588^x \hspace{3.5em}\tag{方程式 3}\)
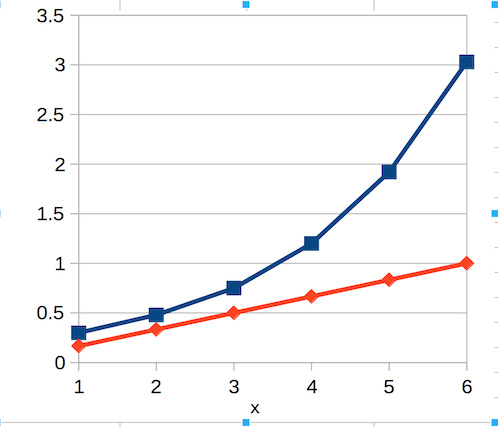
グラフは以下です
対戦結果。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 終盤の手ほど重要視(線形関数) | 0勝8,334敗91,666分 | 61,383勝26,053敗12,564分 |
| 終盤の手ほど重要視(指数関数、小) | 0勝8,863敗91,137分 | 59,992勝25,810敗14,198分 |
| 終盤の手ほど重要視(指数関数、大) | 0勝11,075敗88,925分 | 64,216勝23,404敗12,380分 |
さらに悪化してしまいました(/_;) でも対乱数プログラムでは改善しています。対乱数プログラムで勝率がアップしたのは係数を大きな値にしたことが素直に反映されたのだと思います。
しかし、対最強プログラムの場合では相手は絶対負けないので勝ち点3を得る機会がないので指数関数で係数を大きくしてもあまり恩恵を受けなかったということでしょう。しかも、係数を大きな値にしたために小石(score配列)を補充する際のデフォルト値を10から20に増やす必要があったのです(小石の数がマイナスにならないよう)が、それがよくなかったのだと思います。以前の記事にも書いたように小石の総数を増やすと学習効果が上がらなくなるのです。
もう一つ問題があります。ここでは総手数が6手で終了する場合のデータをもとに作成した回帰方程式を、全ての対戦に使用しています。本来なら総手数毎に動的に計算(LibreOfficeやExcelのgrowth関数のようなものを自作する必要あり?)しなければいけないところを取り敢えず6手の場合で作った方程式を流用して手抜きしているのでよくありません。いい結果に繋がりそうなら追求してみようかと思ってましたが、やってみる価値は無さそうです。
終盤の手ほど重要視すべき?Part 4
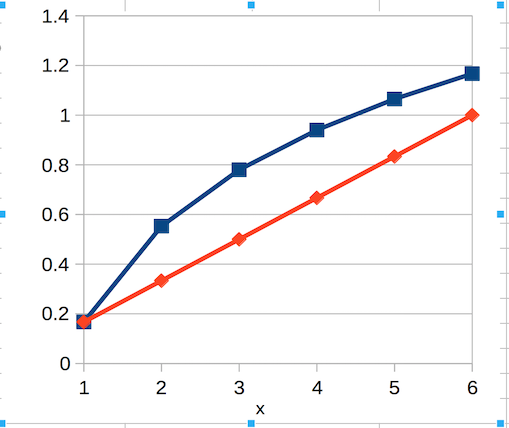
終盤ほど報酬を多くして報酬の総数はなるべく増やさずに曲線で回帰するにはどうすればいいのか考えた結果、対数グラフにしてみました。
「一手の重要度が等間隔で変化するはずがない」から「曲線で推移するはずだ」けど「報酬が増え過ぎると学習効果が薄れる」から「対数関数にしてみよう」という、形から入っただけというかなんとも根拠が薄い感じがしますが、もしかしたらいい結果が出るかもしれないと期待しました。
| x | y (Part1) | y′(Part2) | y′′(Part3) | y′′′ |
|---|---|---|---|---|
| 1 | 0.167 | 0.050 | 0.300 | 0.167 |
| 2 | 0.333 | 0.100 | 0.480 | 0.553 |
| 3 | 0.500 | 0.200 | 0.750 | 0.780 |
| 4 | 0.667 | 0.400 | 1.200 | 0.940 |
| 5 | 0.833 | 0.800 | 1.920 | 1.065 |
| 6 | 1.000 | 1.050 | 3.030 | 1.167 |
それに方程式 2 や方程式 3 の指数関数と違ってこの方程式のいいところは、根拠のない数値から回帰したものではないところです。線形関数の方程式 1 と同様に、総手数と何手目かという変数 x だけで値が決まります。
\(y = \frac{1}{総手数} + \log{x} 総手数 \hspace{3.5em}\tag{方程式 4}\)
根拠がある、無いの話をしだすと、勝ちの時は3を掛けて引き分けは1を掛けるというのはどういう根拠なの?となりますが、これは「STATISTICS HACKS」に書いていたのと、Jリーグなどの多くのスポーツで勝てば勝ち点3、引き分けで勝ち点1となっているので何か(経験則的な?)根拠があるのだろうと思います。
で、対戦結果は以下のようになりました。
| 項目 \ 対戦相手 | 最強プログラム | 乱数プログラム |
|---|---|---|
| 従来の強化学習 | 0勝10,572敗89,428分 | 66,942勝21,791敗11,267分 |
| 終盤の手ほど重要視(線形関数) | 0勝8,334敗91,666分 | 61,383勝26,053敗12,564分 |
| 終盤の手ほど重要視(指数関数、小) | 0勝8,863敗91,137分 | 59,992勝25,810敗14,198分 |
| 終盤の手ほど重要視(指数関数、大) | 0勝11,075敗88,925分 | 64,216勝23,404敗12,380分 |
| 終盤の手ほど重要視(対数関数) | 0勝10,799敗89,221分 | 66,706勝22,489敗10,805分 |
なぜか乱数プログラムに対する勝率はさらに向上しましたが、最強プログラムとの対戦成績は直前の指数関数よりはちょっとましになっただけで、全体として「従来の強化学習」と似たような結果に終わっているので期待はずれでした。この「従来の強化学習」をあらためて説明すると、勝ちは+3、引き分けは+1、負けは−1の値を序盤、終盤関係なく全ての辿った局面データに一律に加減算する強化方法です。いろいろ弄ってみて結局「元の木阿弥」という感じですが、最強プログラムとの対戦成績に関しては終盤に重きを置くことの意味はありそうです。でも、なんで報酬を等間隔に配分した線形方程式(直線)の方が良い成績になるのかは未だに疑問です。
つづく
-
intercept関数とslope関数を使って x と y の表の範囲を指定すれば係数と切片(定数項)が得られます。 ↩