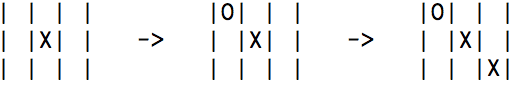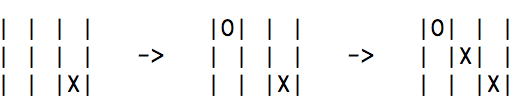無作為選択を人工知能に
「Statistics Hacks」という本の中でココナッツの殻と石ころを使って、学習機能を持つ三目並べプログラムが作れるという話が書かれていました。無人島に漂流して何もすることがない人の暇つぶしのためにどうぞという感じで、非常に砕けた調子で書かれているのです(この本全体がそんな感じです)が、一応裏を取った根拠のある話が書かれている真面目な本だと思います。そして前回の記事で書いたようにBFSアルゴリズムの使い途を考えていた私は「これは使える」と思いました。この本で三目並べについてに書かれている部分はほんの数ページだけなのですが、難しい数式を使っていないので、書かれている内容(アイデア)だけでプログラム作成に必要な情報は十分にあると自分には思われました。但し、その結果強いプログラムが完成するかどうかはやってみないとわからないし、強くなるとしてもどの程度強くなるのか興味が湧いてきたので試してみることにしました。
多分木構造に全局面データを格納
とりあえずBFSで全局面を探索しながら多分木構造のデータを生成し、DBは使わずそのデータをシリアライズして保存(RubyのMarshal.dump)して利用するという方針だけ決めて作業にかかりました。
以下のようなTreeクラスを用意して既に使っているBoardオブジェクト(1局面分のデータ)を格納していきます。メンバー変数valueにデータ(今回はBoardオブジェクト)を格納して、分岐する局面をメンバー変数childに格納していきます。メンバー変数scoreというのは手の良し悪しを評価する得点のことで、上記の本に書いてある石ころの報酬にあたります。それぞれの局面で三目並べの9個のマスに得点(石ころの数)をつけて初期値としてとりあえず10をセットしています。そして勝ち負けに応じて数(石ころの数)を増やしたり減らしたりして良い手悪い手を学習させるつもりです。
class Tree
attr_reader :value, :child, :score
def initialize(v, c=[])
@value = v
@child = c
@score = v.clone
@score.map!{|v|
unless v
v = 10
else
v = 0
end
}
end
#一つ目のパラメータで指定された局面データ(親)を探して、その子ノードとしてオブジェクトを追加する
def add(target, obj)
ret = nil
@child.each_with_index { |c, i|
if c.value == target
ret = c.child.push(obj)
else
ret = c.add(target, obj)
end
break if ret
}
return ret
end
#指定された局面のノードを返す
def search(v)
ret = nil
@child.each { |c|
if c.value == v
ret = c.value
else
ret = c.search(v)
end
break if ret
}
return ret
end
#動作確認用
def parent(v)
ret = nil
@child.each { |c|
if c.value == v
ret = @value
else
ret = c.parent(v)
end
break if ret
}
return ret
end
end
データを作る段階で9箇所のうち駒が打てない場所(すでに駒が存在する場所)のscoreは0をセット(石ころを置かない)しておいて、プラス評価(石ころを増やす)の上限は無いが、マイナス評価(石ころを海に向かって投げる)するときは0未満のマイナス値にはならないように作ります。こうした方が石ころをマイナス個置くなんて現実にはあり得ないということで、本の物語にも沿っていて理解しやすいかもしれません。
データを操作するのは常に木構造の根(ルート,root)から再帰関数を呼び出す形になるので特徴的でシンプルなコードになります。今回はscoreという特殊な要素も付加したのでこのTreeクラスは汎用的なものではなくなってますが、使用するメソッドは多分木を使う時は常に似たような感じ(再帰関数ばかり)になるんじゃ無いでしょうか。
いい加減な数値検証
手始めに前回の記事で作成したbfsメソッドと上記Treeクラスを使って三目並べの局面がどれほどの数になるのか数えようと思い重複チェック(check_dupメソッド)を外して試してみたところ、いつまで経っても処理が終わりません。
board = Board.new([nil, nil, nil, nil, nil, nil, nil, nil, nil])
trees = Tree.new(board)
while queue != [] do
buf = queue.shift
layer = 9 - buf.select{|b| !b}.size
buf.each_with_index {|b, i|
next if b
temp = buf.clone
temp[i] = buf.teban
# next if check_dup(temp)
case layer
when 0
trees.child.push(Tree.new(temp))
else
trees.add(buf, Tree.new(temp))
end
temp.teban = (buf.teban == CROSS) ? NOUGHT : CROSS
set_dup(temp); queue.push(temp)
}
end
仕方なくオブジェクトの作成(newするところ)をコメントにしてカウンターだけ回してみたところ局面の数はなんと986,409となりました。なんとなく最大でも9!(=362,880)で収まると思っていたのですが、この986409という数はどうやら\({}_9 P _1 + {}_9 P _2 + {}_9 P _3 \\\)…\({}_9 P _9 \\\)=(9 + 72 + 504 + 3024 + 15120 + 60480 + 181440 + 362880 + 362880)ということのようです。三目並べ程度のゲームなら静的な配列でもいいかなと思っていたのですがとんでもなかったです。
重複局面を省いて(check_dupメソッドを有効にして)ツリーを生成したところ、局面の総数は初期局面を含めて6,046個になりました。詳細は以下の通りです。
| 手数 \ 重複チェック | 有り | 無し |
|---|---|---|
| 初期盤面 | 1 | 1 |
| 1手目 | 9 | 9 |
| 2手目 | 72 | 72 |
| 3手目 | 252 | 504 |
| 4手目 | 756 | 3,024 |
| 5手目 | 1,260 | 15,120 |
| 6手目 | 1,680 | 60,480 |
| 7手目 | 1,260 | 181,440 |
| 8手目 | 630 | 362,880 |
| 9手目 | 126 | 362,880 |
| 計 | 6,046 | 986,410 |
それにしても986,410から6,046に減るというのもかなりの差で、かなり歪な形のツリー構造になっている感じです。それと下膨れのピラミッド型にならずに手数が増えると空いているマス目が減って重複局面が増えるので、中膨れ状態になるのもやってみなければわからないなぁって感じでした。
世界中で調べ尽くされているであろうゲームなので、いろんなケースの数値を導き出しているサイト1と同じ数値が出せれば検証終了ってことにしようと思ったのですが、なかなかピッタリくるサイトがありませんでした。でも上の表の数値と「tictactoe」という単語で検索するとかなりの数のサイトが引っかかるのでおそらく問題ないでしょう^^;
それと上記の本には287個のココナッツを用意すれば足りると書いてあり、上下左右の対称形を省けばゲームの局面の数は6046ではなくその数にまで絞れるのかもしれませんが、そこまでやるとプログラムが追いにくくなると思ったのでやってません。但し、その数字を出すためにはどうすればいいのか、どうやればその数字で収まることを検証できるか興味はあるので、気が向けば挑戦するかもしれませんが、とりあえず今はまず学習機能作成を進めていこうと思います。
局面を遡るメソッド
本来のBFSの使い途というか迷路の解法の際には、出口に到達した時に入り口まで遡る方法を用意しておかなくてはいけないので、この三目並べのツリーでも最終局面から初手まで遡れるように自分の親を辿るparentメソッドを用意しました。
#verify.rb
require "./constant.rb"
require "./game.rb"
sente_player = Player.new(CROSS, false)
sente_player.init
target = Board.new([-1, 1, 1, -1, -1, -1, 1, nil, 1])
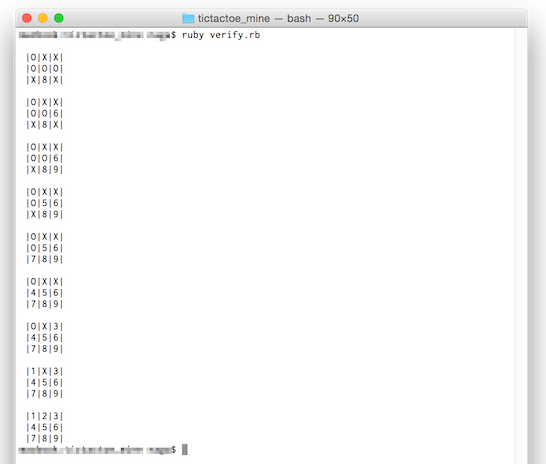
target.display
buf = target
begin
buf = trees.parent(buf)
buf.display
end until buf == nil
上のようにサンプル局面を作ってparentメソッドを呼び出すと下の画面のように手の経過を初手まで辿ることができます。
自分でも作ってから気がついたのですが、迷路の場合なら解答の表示に使えそうなこのメソッドですが、上にも書いてきたように、この多分木データは局面を省略してかなり歪なツリー構造になっているので、parentメソッドを呼び出して自分の局面の一つ前の局面(親データ)に戻ることが出来るといっても、この局面に至った一例を示しているにすぎないということに気をつけなければいけません。三目並べで出現する可能性があるすべての局面データをツリー状態で保持していることは間違いないのですが、その局面に至る手順は本当は幾通りもあるけどデータとして持っているのは一通りだけということです。
1も2も右端の局面は同じで重複データなので一つしか持ってません。だから、1の経過を辿ったのか2の経過を辿ったのか多分木データだけでは知りようがないのですが、それは別途実際に打った手を一つの配列で保持することにします。とにかく出来上がった多分木データはこの例のような子ノードを省いた状態の親ノードが非常に多いということです。
ということで必要になるだろうと思って用意したメソッドですが、parentメソッドは三目並べ機械学習プログラムでは使う必要がなさそうです。ここでも前回同様に迷路の解法と三目並べプログラム作成の違いが出ました。
次の記事で機械学習機能を付けるに当たって新たに必要となった機能について書いていきます。完成したらgithubのソースを更新するつもりです。