「消える三目並べ（Tic-tac-toe Van）」について

　「消える三目並べ（Tic-tac-toe Van）」は、機械学習型三目並べアプリの第二弾です。前作（「進化する三目並べ（Tic-tac-toe Evo）」）は通常の三目並べでしたが、今回は３手前に打った自分の駒が消えるルールの三目並べです。前作は初期データとして全く学習していないデータを使用していましたが、今回の「消える三目並べ」は出現し得る局面の数が通常の三目並べより多いため、初期データとしてある程度学習済みのデータを使用しています。対戦を重ねる度に強くなる点は同じです。

ルール

• ×が先手、○が後手で変更できません。
• 通常の三目並べ同様にラインを揃えれば勝ちですが、３手前に打った自分の駒が消えるのでそれを見越した上で指し手を選択する必要があります。

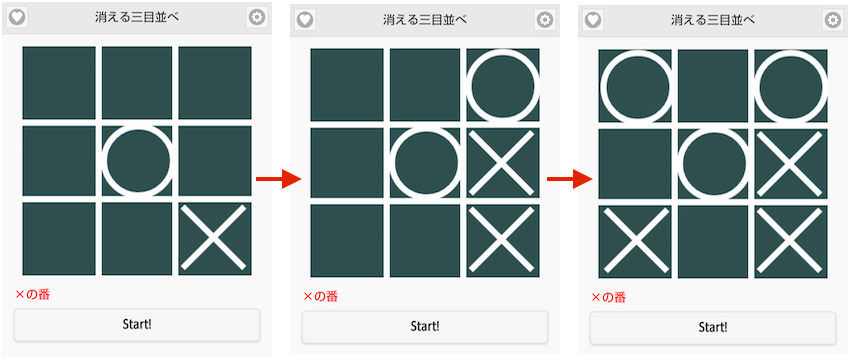
上記のようにゲームが進行した場合、ｘのラインを揃えようとして下段真ん中をタッチしても 三手前の×が消えるので×のラインは揃わず、逆に◯を揃えられて負けてしまいます。

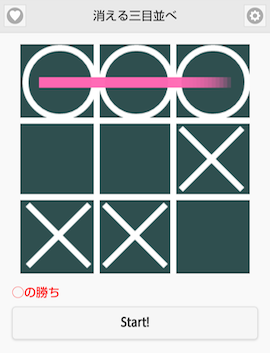
• 引き分けはありません。厳密に言うとゲームの特性上はある限定した局面から先手・後手双方が最善手を続けることで同じ局面の繰り返しに陥る可能性があるのですが、もしそうなってもAI側が手を変えます。

メニュー

• 学習機能

学習機能 On/Off を選択します。Onにするとゲームを終了する度に学習データを書き込むための時間が必要になります

「Saving Learning Data…」のダイアログ表示中に次のゲームを開始する等の操作をすることはタイミング次第で出来なくはないですが、アプリがファイルを書きこんでいる最中はすべての操作が出来なくなります。

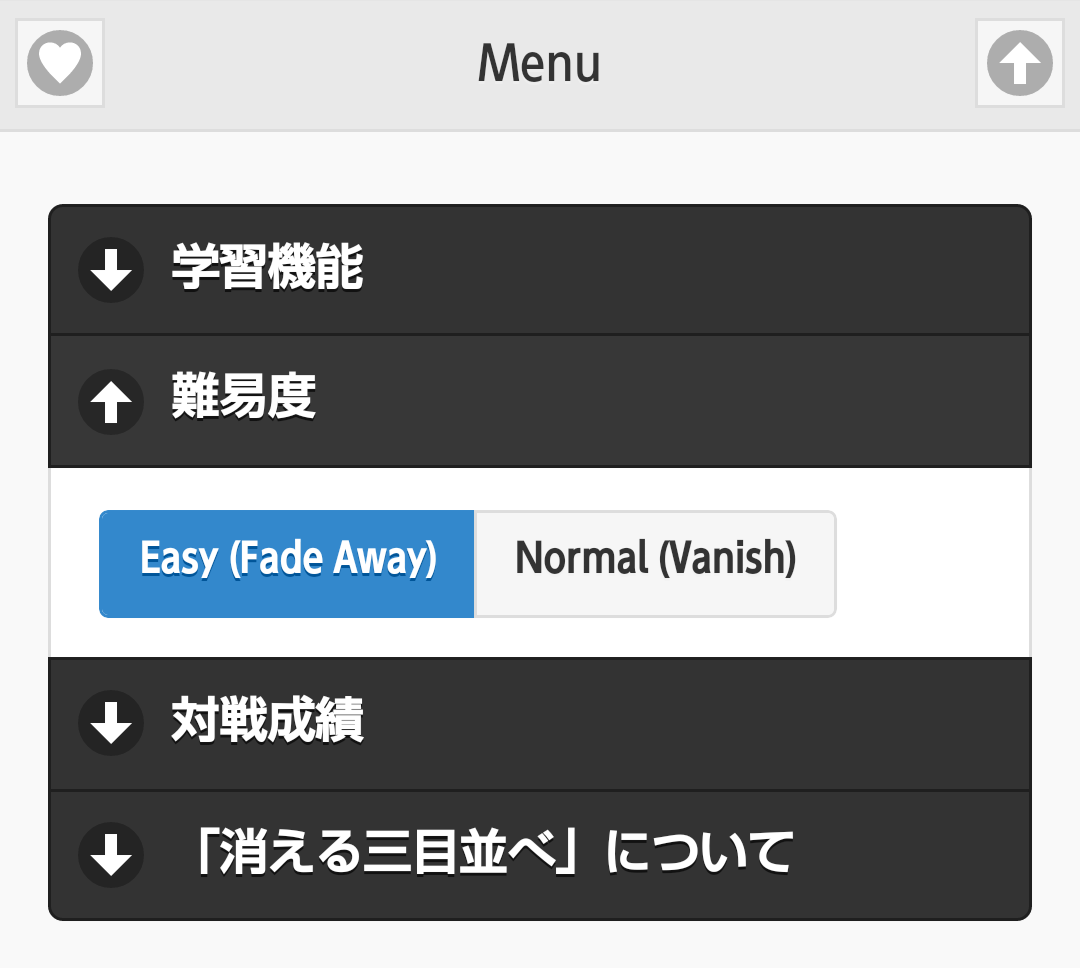
• 難易度
  • Easyモード:
    ３手前に打った駒（×、◯）が徐々に薄くなって消えていく（Fade Away）ので、次にどの駒が消えるか分かるので勝ちやすいです。
  • Normalモード:
    ３手前に打った駒（×、◯）がいきなり消える（Vanish）ので、次にどの駒が消えるか覚えておく必要があるため勝つのが難しくなります。

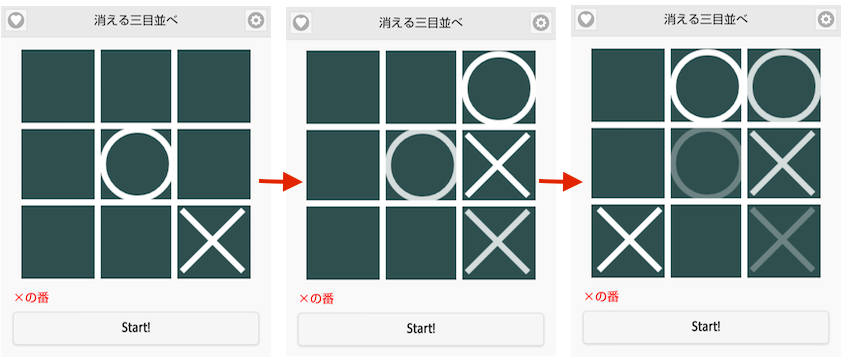
Easyモードに設定した場合、上記のよう古い駒（×、◯）が徐々に薄く描画されます。次にどの駒が消えるか覚えなくてもいいので戦い易くなります。AIの指し手の選択自体はNormalモードもEasyモードも違いはありません。

• 対戦成績

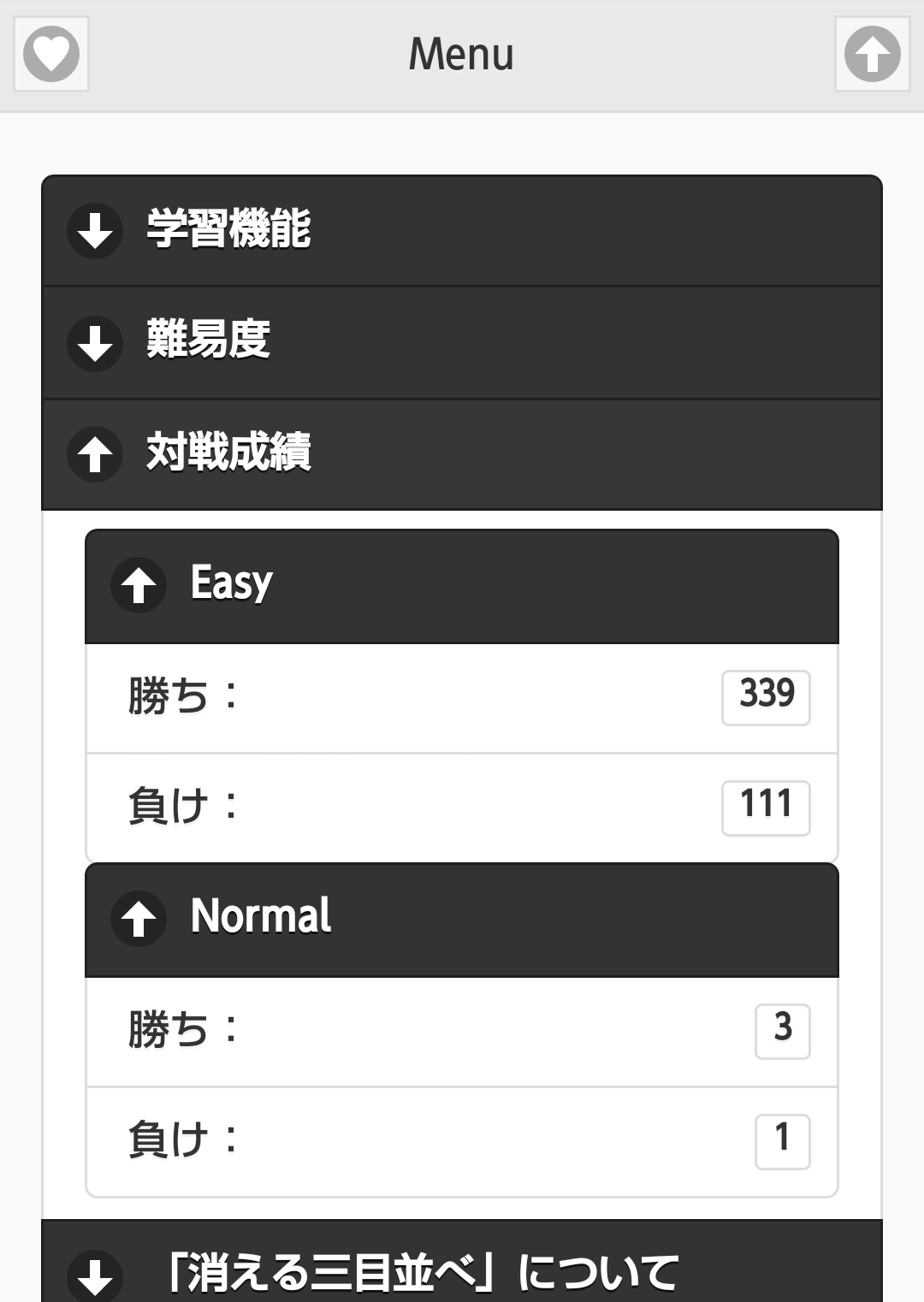
Easyモード、Normalモードそれぞれの対戦成績を表示します。

学習データ

　AI用の初期データとしてある程度学習済みのデータ（MIN-MAX法を使った最強プログラムと10,000回対戦させたデータ）を使用しています。以下のグラフはまったく学習させていないところから乱数プログラムと最強プログラムの２種類のプログラムと対戦テストを行って、アプリの勝率の推移をグラフにしたものです。グラフの黄色のラインの経過を経たデータを初期データとしてアプリに同梱しています。最強のプログラムに対して勝率５割には達していませんので、初心者の方でも全く勝てないなんてことはないと思います。

元に戻す　※範囲をドラッグすれば、グラフを zoom up 出来ます

　手数の推移は参考程度に見て下さい。グラフではわかりにくいほどの微妙な違いですが、最強プログラムと対戦テストを行った場合（水色のグラフ）、最初は最強プログラムに対して短手数で簡単に負けていたアプリが学習が進むに連れてなかなか負けないようになり手数が徐々に伸びていっていることがわかります。また、乱数プログラムと対戦テストを行った場合（緑色のグラフ）はお互いに弱い者同士なのでなかなか決着が付かずにゲーム終了までに無意味に長い手数が必要だったものが、学習を積み重ねることによってアプリ側が勝ち方を覚えていき、ゲーム終了までの手数が徐々に短くなっていくことが見て取れます。
　プロットするのが大変なのでグラフにはしていませんが、対乱数プログラムとの対戦グラフ（赤色のグラフ）は100,000回までテスト回数を伸ばすと９割以上の勝率にまで伸びることを確認しています。このグラフの１０倍の回数対戦させて９割ですので、かなり緩やかな右肩上がりのグラフです。対最強プログラムのグラフも（黄色のグラフ）も同様に緩やかな右肩上がりに推移すると思われます。