インプライド・ボラティリティ(IV)とヒストリカル・ボラティリティ(HV)
ボラティリティには2種類ありますが、ニュースの記者や市況解説者が「ボラティリティ」という言葉を理解していないまま使っていることが多いと感じるので、以前から一言言っておきたいと思っていたことを書いておこうと思います。
市況解説の中でも現物市場ではなく特に先物市場の解説をしている人が、先物価格の値動きが荒かった日などに「今日はボラの大きな一日でした」と解説しているのを聞くと「(・_・)……ン?」となることがあります、そういう日でもインプライドボラティリティ(IV)が低い日も結構あるからです。オプションの買いで勝負する時はボラが高い時が有利、逆に売りはボラが低い時が有利なのですが、IVが低い日に「今日は(オプション買いに)手出ししなくてよかった」と思っているところに、市況解説で「ボラの高い一日でした」なんて言われると「(‾△‾;)エッ・・そうだっけ?」となるわけです。実際にIVが高かったかどうかはスマイルチャートなどで確認できます。
直近1年のボラティリティーをみればよく分かりますが、ヒストリカル・ボラティリティ(HV)とインプライド・ボラティリティ(IV)の動きは必ずしも一致していません。原資産である先物の動きがそれ程なくても、オプションの値動きが激しい日もあるということです。それにオプションは先物と違い、満期(SQ)が近づくとボラ(IV)が高くなるという性質(時間価値の減少に伴うもの)もあります。また、日経225先物とそれを原資産とする派生商品である日経225オプションの関係だけでなく、現物株とそれを原資産とする派生商品(株オプ等)の間でも同じことが言えます。
まぁIVとHVの違いは理解しているけど、ボラティリティと言う言葉は単に「値動き」とか「値幅」と同義で使っているだけなので、区別する必要はないと言われればそれまでなのですが。
誤解を生む説明の仕方
ネットや本ではよく「ボラティリティが高いとオプションのプレミアムが高くなる、ボラティリティが低いとオプションのプレミアムが低くなる」と説明されています。でもこの文を読んでいる人を騙そうとする悪意があるかどうかは別にして、非常に誤解を生みやすい説明だと思います。なぜなら、ボラティリティが高いとという前提条件がIVのことを指しているのかHVのことを指しているのかわかりません。
もしIVのことを指しているとしたら、IVが高いとプレミアムが高くなるのはその通りですが、そのIVというものはオプションの価格から算出されているものだから当たり前のことを言っているに過ぎません。IVが高いとオプションのプレミアムが高くなるわけではなく、IVが高いってことはオプションが割高に買われているってことです。
また、ボラティリティが高いとという前提条件がHVのことを指しているのだとすると、HVが高いとオプションの理論価格が高くなることは間違いないですが、オプションの実際の価格が理論価格通りに高くなるとは限りません。HVが高いとオプションの価格(プレミアム)が高くなるのではなく、HVが高いとオプションの理論価格が高くなると言うべきです。
ボラティリティが高いとという表現がIVのことを指しているとしてもHVのことを指しているとしても、いずれも不正確な文章だと言えます。IVとHVの違いを理解している人でもつい説明する手間を省いて、こういう表現をしがちなんだと思いますが、説明する側がよく理解していないケースも多いと思います。
違いが分かる説明の仕方
Wikipediaによるボラティリティの説明は学問的で、これはこれでいいのかもしれません。それに「インプライド・ボラティリティとは現実のオプション市場でついたオプション価格から逆算されたボラティリティのことである」とこれ以上望めない簡潔な言葉で言い表されています。
しかし、これ
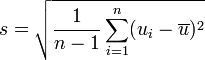
とか、
こういう
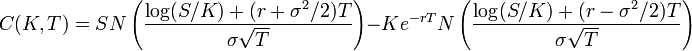
難しい数式が出てくるので、「要するにどちらも値動きの荒さ、変動率のことだろ?」と言う感じで思考を中断してしまいがちだと思うのです。オプションという商品を理解しているつもりだった自分も、先物・オプション売買損益シミュレーションサイトを自分で作ってみるまではIVとHVの違いを明確に区別出来ていなくて、よく似たような物ぐらいに考えていました。
そこで、
ヒストリカル・ボラティリティ\(x\)とオプション理論価格\(y\)は以下のように表すことが出来て、
オプションの実際の価格が\(y_1\)であった時に、導き出されるものがインプライド・ボラティリティ\(x_1\)である。
という感じで簡略化した数式を書いてくれれば2つのボラティリティの関係が分かり易くなると思うんですけど、どうでしょうか?